
 |
DETERMINANTES |
La idea de determinante es una concreción de
la idea de matriz, es decir, no tiene sentido si no es a través
de una matriz cuadrada. Se trata de asignarle a cada matriz un
valor de R que, de alguna forma, la representa.
Sin embargo, antes de definir lo que es un determinante, necesitamos tener en cuenta algunas definiciones relativas a conceptos que vamos a utilizar en la definición.
Una permutación de n elementos es una
aplicación biyectiva de ![]() en
en ![]() de la siguiente forma:
de la siguiente forma:

Como el elemento inicial no suele ser importante en una permutación (están ordenados como 1, 2, 3, ...,n) se acostumbra a identificar la permutación con el elemento resultante (la imagen de la aplicación).
Así, (1, 7, 4, 2, 5, 6, 3) es una permutación de 7 elementos, donde, la aplicación es tal que:
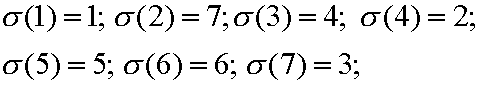
No hace falta recordar que las permutaciones
de n elementos dan como resultado n! elementos distintos.
Ejemplo: Las permutaciones posibles con {1, 2,
3} son 3! = 6 y son:
![]()
![]()
![]()
![]()
![]()
![]()
Se dice que los elementos h y k de la
permutación s forman
una Inversión cuando h < k y s(h) > s(k), es
decir, cuando, tras la permutación, se pierde el orden creciente
en relación a estos dos elementos.
Ejemplo: ![]()
3 y 2 forman una inversión, y 3 y 1 forman
otra inversión.
Dada una permutación s,
si contamos el no de inversiones
que hay en ella, podemos indicar el Índice de la
permutación de la siguiente forma:
El índice de s será
1 si el no de inversiones es par.
El índice de s será
-1 si el no de inversiones es
impar.
Se puede resumir así: ![]()
Ejemplo: La permutación (3, 4, 2, 1, 5)
tiene índice –1, ya que el no
de inversiones que tiene esta permutación es 5 (que son 3,2 ;
3,1 ; 4,2 ; 4,1 ; 2,1)
Dada una matriz cuadrada de orden n :
A =
Se llama Determinante de A y se representa
por |A| ó también det(A), al número que se obtiene de la
siguiente forma:
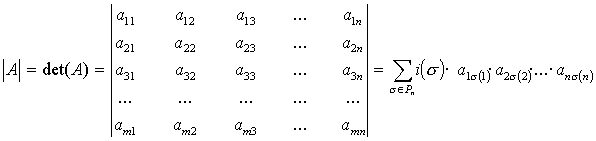
![]() son las
distintas permutaciones de n elemento (es decir, n! elementos)
son las
distintas permutaciones de n elemento (es decir, n! elementos)
Por tanto,
el determinante de una matriz de orden n estará
formado por la suma de n! sumandos, cada uno de ellos
formado por n factores, entre los que figura un solo elemento de
cada fila y un solo elemento de cada columna de la matriz.
Vamos a ver qué significa esta definición en matrices de orden pequeño:
q Determinantes de orden 1:
Si ![]() es
una matriz de orden 1,
es
una matriz de orden 1, ![]()
El valor del determinante coincide con el valor del único elemento de la matriz.
q Determinantes de orden 2:
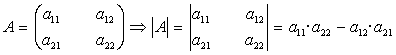
El primer término ![]() lleva
signo + porque la permutación de los índices de las
columnas (1, 2) es par.
lleva
signo + porque la permutación de los índices de las
columnas (1, 2) es par.
El segundo término ![]() lleva
signo - porque la permutación de los índices de las
columnas (2, 1) es impar.
lleva
signo - porque la permutación de los índices de las
columnas (2, 1) es impar.
q Determinantes de orden 3:
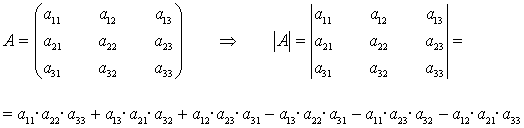
En el desarrollo aparecen 3!=6 sumandos. En
cada uno de ellos intervienen 3 factores entre los que hay un
solo elemento de cada fila y un solo elemento de cada columna.
Cada sumando va precedido del signo + ó – según la paridad
de la permutación formada por los índices de columnas. Así, el
término ![]() lleva signo menos ya que la
permutación (2, 1, 3) es impar.
lleva signo menos ya que la
permutación (2, 1, 3) es impar.
Para recordar fácilmente la expresión que permite calcular el valor de un determinante de orden 3 se utiliza la regla de Sarrus, que identifica gráficamente cómo elegir los factores:
|
Para ver en qué consiste gráficamente la regla de Sarrus, pulsa el botón Animar |
| Ejercicio:
calcula el valor del determinante buscando todas las
posibles permutaciones de los elementos de la matriz A. A
continuación, comprueba el resultado obtenido con el
módulo Descartes. |
| Fernando Villarrubia Gahete | ||
|
© Ministerio de Educación y Ciencia. Año 2003 |