1.- El determinante de una matriz cuadrada es igual al determinante de su traspuesta.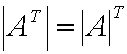, ya que al cambiar las filas por las columnas los productos quedan iguales y con igual signo.

 

Ejercicio: Comprueba con la definición de determinante que esta propiedad se cumple gracias a la propiedad conmutativa del producto, ya que las ternas de números son iguales salvo el orden. 

 

2.- Al intercambiar dos líneas paralelas (filas o columnas) de una matriz, el determinante cambia de signo, pero no varía su valor absoluto (ya que todos los elementos cambian de índice en la permutación).  

Filas

Columnas

 

Asimismo, cambia el signo si se hace un no impar de intercambios de líneas paralelas. El signo se mantiene si el no de intercambios es par.

Ejercicio: Calcula el valor del determinante de A. A continuación mueve las filas de la siguiente forma: la fila 1 pasa a ser la fila 2, la fila 2 pasa a ser la fila 3 y la fila 3 pasa a ser la fila 1. ¿Qué signo tendrá el determinante resultante? Anota en tu cuaderno el resultado e interpreta por qué es ese el signo obtenido.
  Fernando Villarrubia Gahete  
© Ministerio de Educación y Ciencia. Año 2003