parábolas1

	Las parábolas y=a x²+ k.
	4º de E.S.O. Opción B.

4.- Las parábolas y = ax².

En la siguiente escena está dibujada en color rojo la parábola de ecuación y=x².

Cambiando el valor de a, podrás ver las gráficas de funciones como por ejemplo y= -x², y= 3x², y= -(1/2)x², y= 2x² etc.

Observa cómo influye el valor de a en la forma de la parábola. La parábola y=2x² es más ancha es decir, se aleja del eje OY más que la de ecuación y=3x².

Escena 1

Modifica los valores de a y observa lo que ocurre si introduces números negativos.

En la escena aparece una tabla de valores para las funciones: y=x²
e
y=a x²


EJERCICIOS. 7.- En tu cuaderno, responde a las siguientes preguntas: a) ¿Qué parábola es más ancha y=-3x² ó y=0.2x² ? b) ¿Qué parábola es más estrecha y=2x² ó y=0.5x² ? c) Clasifica por la forma de sus gráficas las parábolas y=2x² , y=1.5x² , y=-x² y=-3x² , y=-2.3x² , y=4x² .

Observa: Si a>0, la parábola tiene la forma: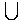 . Se dice que es cóncava hacia arriba. Si a<0 ,la parábola tiene la forma: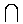 .Se dice que es cóncava hacia abajo. Conforme mayor sea a en valor absoluto, la parábola es más estrecha es decir, más cercana al eje OY. La función y=ax² tiene las siguientes características: >Su Dominio es R. >Es simétrica respecto al eje OY, ya que f(-x)=f(x). >Es una función continua >Si a>0, la función es decreciente para x<0 y creciente para x>0. Tiene, por tanto, un mínimo en (0,0) que es el vértice de la parábola. >Si a<0, la función es creciente para x<0 y decreciente para x>0. Tiene, por tanto, un máximo en (0,0) que es el vértice de la parábola.

5.- Las parábolas y =a x² + k.

En la siguiente escena, si fijas el valor de a=1, aparecerá dibujada en color rojo la parábola de ecuación y=x², y en color azul las parábolas de ecuación y=x²+k.

Cambiando el valor de k, podrás hacer investigaciones y relacionar las gráficas de las funciones y=x²+k con la de y=x².

A continuación, trabaja cambiando también el valor de a.

Observa cómo puedes representar funciones como y=x²+3, y=x²+7, e y=x²-4 a partir de la función y=x².

Escena 2

Utilizando los controles a y k, podrás representar las gráficas de las funciones : y =ax²+k.

Utiliza el control x para hacer una tabla de valores que te ayude en tus investigaciones.

El vector de origen P puede moverse por la escena.

Observa cómo:

La gráfica de y = x²-2 se obtiene trasladando hacia arriba la gráfica de la función y = x²,2 unidades hacia abajo.

A partir de la gráfica de y = - x², se obtiene la de y = - x²+1 trasladando la inicial 1 unidad hacia arriba.

EJERCICIOS.

Utilizando lo que has aprendido en esta unidad, realiza en tu cuaderno los siguientes ejercicios:

8.- A partir de la gráfica de y=x², representa las gráficas de y=x² -1, y=x² +3,y= x² +2 e y=x²-0.5.

9.- A partir de la gráfica de y=-x², representa las gráficas de y=-x² +0.5, y=-x² +3, y= -x² +2 e y=-x²-1.

10.- A partir de la gráfica de y=2x², representa las gráficas de y=2x² -1,y=2x² +3, y= 2x² +2 e y=2x²-0.5.

11.- A partir de la gráfica de y=-3x², representa las gráficas de y=-3x² +1, y=-3x² +2, y= -3x² -2 e y=-3x²-0.5.

La gráfica de la función y=ax²+k, se puede trazar a partir de la gráfica de y=ax² , trasladando ésta, k unidades hacia arriba si k>0 o bien trasladándola k unidades hacia abajo si k<0.

	Constanza Irizo Gaviño

	© Ministerio de Educación y Ciencia. Año 2004