Infinitesimos1

1. LOS INFINITÉSIMOS

Análisis.

Bachillerato de la modalidad de Ciencias de la Naturaleza y de la Salud o Tecnológico

1.1 INFINITÉSIMO

Se dice que la función f es un infinitésimo cuando x → a, si se verifica

Es decir, un infinitésimo es una función cuyo límite es cero cuando la variable independiente x se aproxima hacia el valor x = a, o dicho de otra forma, una función cuyos valores se aproximan tanto más al cero cuanto más se aproxima x hacia el valor a.

Por tanto, en el concepto de infinitésimo hay que tener presente no sólo la función f, sino también el punto a. La función f es infinitésimo, en las proximidades del punto a. Suele decirse que es infinitésimo en x=a.

En la escena de la izquierda se puede observar que, por ejemplo, las funciones

f(x) = x

g(x) = 1-cos(x)

h(x) = ½x²

son infinitésimos en x = 0,

mientras que la función

k(x) = -x²+4x-4

lo es en x = 2.

Comprueba:

Utiliza el puntero del ratón o el control x para mover la variable independiente x por el eje de abscisas y comprobar lo que se dice.

Puedes desplazar si lo deseas los ejes por medio de los controles 0.x y 0.y, así como utilizar el zoom.

Algunas propiedades de los infinitésimos:

a) Si f y g son infinitésimos , entonces f ± g, y f · g son también infinitésimos.

b) El producto de un infinitésimo por una constante, o por una variable acotada, es un infinitésimo.

c) El cociente de un infinitésimo f por una constante no nula, o por una variable h(x) con |h(x)| > M > 0, es un infinitésimo.

1.2 COMPARACIÓN DE INFINITÉSIMOS

Al comparar infinitésimos se puede observar la rapidez con la cual tienden a cero.

Por ejemplo, en la escena de la izquierda, de las tres funciones que aparecen (infinitésimos cuando x tiende a cero), si observamos la rapidez con la que se aproximan a cero, se puede afirmar que:

f(x) = x es la que tiende a cero menos rápidamente.

g(x) = 1-cos(x) y h(x) = ½x² lo hacen con igual rapidez.

Diremos entonces que

g y h son infinitésimos de orden superior a f,

ellos dos entre sí son infinitésimos del mismo orden,

y que f es un infinitésimo de orden inferior a g y

Comprueba:

Utiliza el puntero del ratón o el control x para mover la variable independiente x por el eje de abscisas y comprobar lo que se dice. En la escena aparecen también los valores que toma cada función para cada valor de x. Haz uso de ello para ratificar lo dicho.

En general, se da la siguiente definición:

Si f y g son infinitésimos cuando x → a, se dice que

f es infinitésimo de orden superior, igual o inferior que el infinitésimo g, si es , respectivamente, igual a 0, igual a un número finito k ≠ o igual a ∞.

Ahora puedes confirmar cómo son entre sí los infinitésimos estudiados antes:
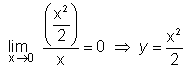es un infinitésimo de orden superior a y = x.	Tarea 1: Mediante el cálculo de límites confirma en tu cuaderno que efectivamente el valor de esos límites es el que se indica:
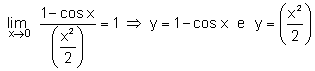es un infinitésimo de orden superior a y = x.
son infinitésimos del mismo orden.
Obviamente, invirtiendo los dos primeros límites se tendría el tercer caso de la definición.

	Cándido Teresa Heredia

	© Ministerio de Educación y Ciencia. Año 2004