FRACCIONES, RACIONALES E IRRACIONALES
Álgebra
 
3.- Todas las fracciones son números racionales (Q)

Una fracción es una división de números ENTEROS. Veamos cómo pueden ser los resultados de esa división.

Introduce en esta escena las siguientes fracciones:
a) 72/9 c) 4/11
b) 197/40 d) 87/66

Puedes introducir también cualquier otra fracción.

En tu cuaderno

3a) ¿Cuántos tipos de números distintos resultan?

3b) Identifica los cuatro resultados obtenidos con cada uno de los cuatro tipos de números que exponemos a continuación:

1.- NÚMERO ENTERO.- Ocurre cuando el numerador es múltiplo del denominador.
2.- DECIMAL EXACTO.- Tiene un número finito de decimales. Ocurre cuando en una fracción irreducible los factores primos del denominador sólo son el 2 y el 5.
3.- DECIMAL PERIÓDICO PURO.- Tiene infinitas cifras decimales periódicas. Un grupo de cifras se repite desde la coma. En el denominador hay otros factores que no son el 2 o el 5.
4.- DECIMAL PERIÓDICO MIXTO.- Tiene infinitas cifras decimales periódicas, pero tiene algunas cifras decimales que no se repiten. En el denominador hay otros factores que no son el 2 o el 5.

 

TODO NÚMERO QUE SE PUEDA PONER EN FORMA DE FRACCIÓN DE DOS ENTEROS ES UN NÚMERO RACIONAL. Forman el conjunto Q de los números racionales.
4.- Los números irracionales
Los números que tienen infinitas cifras decimales no periódicas, no se pueden poner en forma de fracción y se llaman IRRACIONALES

Son irracionales los siguientes números:
A.- Radicales no exactos: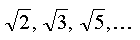

En esta escena puedes ver una forma de dibujar los radicales de los diez primeros números naturales.

En tu cuaderno

4a) ¿Cuáles de ellos son racionales y cuáles irracionales?

Fíjate bien como son los triángulos que se dibujan cada vez que pulsamos el control de la escena, y cuánto valen sus lados.

4b) Continúa el dibujo en tu cuaderno con varios triángulos más.

4c) A este dibujo se le llama CARACOL PITAGÓRICO. ¿Por qué será?

Puedes arrastrar con el ratón los extremos de cada segmento para situarlos en la recta.
A cada número irracional también le corresponde un punto de la recta

B.- El número Pi = 3.14159...

C.- El número e = 2.71828...

D.- El número de oro Phi = 1.618033...

4d) ¿En qué ocasiones, o qué estabas estudiando cuando te has encontrado con estos tres números irracionales?
  Volver al índice   anterior   siguiente  
           
  Juan Madrigal Muga y Ángela Núñez Castaín
 
© Ministerio de Educación y Ciencia. Año 2003