REPRESENTACIÓN DE FUNCIONES LOGARÍTMICAS
Análisis
 

Representar la función:  y=ln(x2-1)

1. INFORMACIÓN EXTRAÍDA DE LA FUNCIÓN

1) Dominio

  • El ln de x2-1 no existe desde -1 a 1, ya que sólo existe el logaritmo de los números positivos, luego la función está definida en (-¥,-1) y en (1,¥)

2) Cortes con los ejes y signo

  • Con el eje OY: cuando x=0 la función no está definida luego no tiene corte con este eje.

    Con el eje OX: resolvemos la ecuación ln(x2-1)=0, es decir (x2-1)=1  resultando las soluciones x=-Ö2, y x=Ö2

x (-¥,-Ö2) -Ö2 (-Ö2,-1) [-1,1] (1,Ö2) Ö2 (Ö2,¥)
y + 0 -   - 0 +

Cambia el valor de x en la escena o arrastra el punto rojo con el ratón, podrás ver los valores que toma y=f(x). Observa como en el intervalo [-1,1] la función no alcanza ningún valor.

3) Simetría

  • Se trata de una función PAR ya que
    f(-x)=    ln((-x)2-1)=f(x) por tanto es simétrica respecto al eje de ordenadas.

4) Asíntotas

  • VERTICALES, las rectas x=-1 y x=1 ya que

            

  • HORIZONTALES, no hay puesto que

  • En este caso tampoco hay OBLICUAS

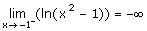
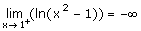
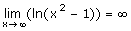
Cambia el valor de x o arrastra el punto rojo con el ratón acercándote a 1 o a -1, para comprobar que cuando x®-1-  y®-¥ ; y que cuando x®1+ y®-¥

 
       
           
  María José García Cebrian
 
© Ministerio de Educación y Ciencia. Año 2001