
Propiedades operativas de los límites infinitos III.
 |
Propiedades de los límites: Propiedades operativas de los límites infinitos III. |
| 2º de Bachillerato CCNN y Tecnológico. Análisis. | |
| Cociente entre un límite infinito y un límite finito no nulo. | |
|
"Sean f una función con límite infinito en el punto a y g(x) una función con límite finito no nulo en el mismo punto a (llamaremos b a este límite, con b distinto de cero). Entonces la función f/g tiene límite infinito en el punto a si b es positivo, límite menos infinito si b es negativo".
Es decir
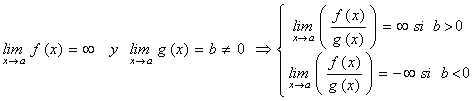
|
|
Manipula la gráfica lo necesario para contestar a las preguntas que se plantean a continuación.
| ||
|
1.- Modifica el valor de p hasta conseguir que b sea positivo. Una vez hecho esto halla un valor de m que sea una cota superior de g(x) en las cercanías del punto a. ¿Es siempre posible encontrar un tal valor m? ¿Por qué? Halla a continuación un valor d para el que se cumpla que si x dista de a menos que d, con toda seguridad g(x) es menor que el valor m anterior. Anota el valor de d obtenido. | ||
|
2.- Selecciona ahora un valor de K positivo tan grande como quieras. Averigua para qué valor de d se cumple que si x dista de a menos que d con toda seguridad f(x) es mayor que mK, siendo m el valor obtenido en el apartado anterior. Anota el valor obtenido. ¿Es siempre posible encontrar un valor d que cumpla esta condición? ¿Por qué? | ||
|
3.- Haz ahora que d tome el valor más pequeño de los dos que has obtenido y contesta a la siguiente cuestión. Si x está dentro del intervalo limitado por las rectas verticales azules f(x) es mayor que mK y 1/g(x) es mayor que 1/m (¿por qué?) ¿qué puede afirmarse de (f*g)(x) y K? | ||
|
4.- Repite los pasos anteriores dando distintos valores a K, cada vez mayores. | ||
|
5.- Modifica ahora el valor de p hasta conseguir que b sea negativo. Una vez hecho esto halla un valor de m que sea negativo y al mismo tiempo una cota superior de g(x) en las cercanías del punto a. ¿Es siempre posible encontrar un tal valor m, con tal de que b sea negativo? ¿Por qué? Halla a continuación un valor d para el que se cumpla que si x dista de a menos que d, con toda seguridad g(x) es menor que el valor m anterior. Anota el valor de d obtenido. | ||
|
6.- Selecciona ahora un valor de K negativo tan pequeño como quieras. Averigua para qué valor de d se cumple que si x dista de a menos que d con toda seguridad f(x) es mayor que mK, siendo m el valor obtenido en el apartado anterior (observa que al ser tanto K como m negativos, el producto mK será positivo). Anota el valor obtenido. ¿Es siempre posible encontrar un valor d que cumpla esta condición? ¿Por qué? | ||
|
7.- Haz ahora que d tome el valor más pequeño de los dos que has obtenido y contesta a la siguiente cuestión. Si x está dentro del intervalo limitado por las rectas verticales azules f(x) es mayor que mK y 1/g(x) es mayor que 1/m (¿por qué?) ¿qué puede afirmarse de (f/g)(x) y K? | ||
|
8.- Repite los pasos anteriores dando distintos valores a K, cada vez menores. | ||
|
Si has contestado satisfactoriamente a las preguntas anteriores habrás obtenido que sea cual sea el valor de K (K positivo si b es positivo y K negativo si b es negativo) es posible encontrar otro número positivo d tal que si la distancia entre x y a es menor que d, entonces g(x) es menor que una cierta constante positiva m si b es mayor que cero; g(x) es menor que una cierta constante negativa m si b es menor que cero y, en ambos casos, f(x) es mayor que mK y 1/g(x) es mayor que 1/m, por lo tanto para esos valores de x (f/g)(x) será mayor que K si b es positivo y menor que K si b es negativo. | ||
| Cociente de un límite finito entre un límite infinito. | |
|
"Sean f y g dos funciones: f con límite finito en el punto a (al que llamaremos b) y g con límite infinito en a. Entonces la función f/g tiene límite cero en a".
Es decir
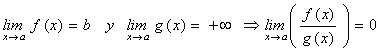
|
|
Manipula la gráfica lo necesario para contestar a las preguntas que se plantean a continuación.
| ||
|
1.- Modifica el valor de p hasta conseguir que b sea positivo. Una vez hecho esto halla un valor de K que sea una cota superior de f(x) (y -K una cota inferior) en las cercanías del punto a. ¿Es siempre posible encontrar un tal valor K? ¿Por qué? Halla a continuación un valor d para el que se cumpla que si x dista de a menos que d, con toda seguridad |f(x)| es menor que el valor K anterior. Anota el valor de d obtenido. | ||
|
2.- Selecciona ahora un valor de e positivo tan pequeño como quieras. Averigua para qué valor de d se cumple que si x dista de a menos que d con toda seguridad g(x) es mayor que K/e, siendo K el valor obtenido en el apartado anterior. Anota el valor obtenido. ¿Es siempre posible encontrar un valor d que cumpla esta condición? ¿Por qué? | ||
|
3.- Haz ahora que d tome el valor más pequeño de los dos que has obtenido y contesta a la siguiente cuestión. Si x está dentro del intervalo limitado por las rectas verticales azules |f(x)| es menor que K y 1/g(x) es menor que e/K (¿por qué?) ¿qué puede afirmarse de (f/g)(x) y e ? | ||
|
4.- Repite los pasos anteriores dando distintos valores a e . Repite, después todo el proceso haciendo b=0 y haciendo b negativo. | ||
|
Ejercicios.
¿Qué sucederá en el primer caso si f tiende a menos infinito? ¿Y en el segundo caso? Razona las respuestas.
| ||
| José Luis Alonso Borrego | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2001 | ||