|
6.
PRODUCTO ESCALAR
|
|
DEFINICIÓN
|
|
El producto escalar de dos vectores se define
como el producto de los módulos por el coseno
del ángulo que forman
u.v=|u|*|v|*cos(u,v)
Los módulos de los vectores son
números, y el coseno también, por tanto el
producto escalar es un número.
|
|
PROPIEDADES
DEL PRODUCTO ESCALAR
|
1.-  ,
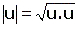pues 
|
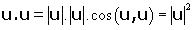
2.-  ,
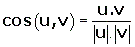basta despejar el coseno, de la definición de producto escalar
|
|
3.- Si u=0
o v=0
entonces u.v=0
|
4.- Si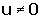 
y 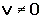 Y
u. v = 0
a
u
^
v (perpendiculares),
pues u. v = |u|. |v|. cos 90º = 0
|
5.- La proyección de u
sobre v
es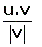 
|
|
En
la escena puedes ver como se dibuja pulsando 
y dando al pulsador pasos verás la demostración. |
|
|
|
6.- Conmutativa
u.v = v.u
|
|
7.- Asociativa (k.u).v
= k. (u.v), siendo u
y v
vectores y k
un número real.
|
|
8.- Distributiva u.
(v + w) = u. v + u. w
|
9.- Si B
(i, j, k) es una base ortonormal,
se cumple que:
| i. i = 1 |
i. j = 0 |
| j. j =1 |
i. k = 0 |
| k. k = 1 |
j. k = 0 |
Ya que i,
j, k son perpendiculares y sus
módulos |i| = |j| = |k| = 1
|
|
10.- EXPRESIÓN
ANALÍTICA DEL PRODUCTO ESCALAR.-
Si las coordenadas de u
y v son
u(x1, y1, z1)
y v(x2, y2, z2)
respecto de una base ortonormal B (i,
j, k), entonces u.
v = x1. x2 + y1. y2 + z1.
z2
|
