
 |
FUNCIONES: Concepto de función. |
| 1º de Bachillerato HH y CCSS. Análisis. | |
| 1. Análisis de los ejercicios anteriores. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Vamos a analizar ahora qué es lo que tienen en común las tres situaciones planteadas en la página anterior.
En el primer caso (estudio de desplazamientos), la información que hemos analizado venía expresada en forma gráfica. Esas gráficas establecían una relación (numérica en este caso) entre dos magnitudes: el tiempo (medido en minutos) y la distancia (medida en km). Como puedes comprobar, en las cuatro gráficas se verifica que en un determinado instante, t, el punto que representa la distancia recorrida no puede estar en dos posiciones diferentes. En otras palabras, a un valor determinado de t le corresponde un valor y sólo uno de la distancia.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Observa que lo contrario no es necesariamente cierto: en una de las gráficas se produce la siguiente situación: una distancia determinada es alcanzada en dos instantes de tiempo diferentes. ¿En qué gráfica se da esa situación? ¿En qué se ve que se da esa situación? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Lo contrario, en cambio, no siempre es cierto: observa la tabla 1. El número medio de crías puede ser de 2,0 a una temperatura de 15º y a una temperatura de 25º. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Tabla 1.
Tabla 2.
Tabla 3.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. Definición de función. | |
|
Todo esto nos lleva a la siguiente definición: "Una función es una ley que relaciona dos magnitudes númericas (llamadas variables) de forma unívoca, es decir, que a cada valor de la primera magnitud (llamada variable independiente) le hace corresponder un valor y sólo uno de la segunda magnitud (llamada variable dependiente). Suele decirse que la segunda magnitud es función de la primera."
Utilizando estas expresiones en nuestros ejemplos, diremos que la distancia recorrida por los alumnos del primer caso es función del tiempo que han empleado en recorrerlo; el porcentaje de distribución de la riqueza de un país es función del porcentaje de población que la detenta; el número medio de crías de la pulga de agua dulce por hembra y día es función de la temperatura del agua en que viven.
Todos los ejemplos analizados nos permiten ver que a pesar de tratarse de situaciones completamente diferentes todas pueden expresarse simbólicamente de la misma forma: 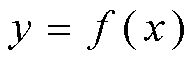 donde x representa la variable independiente e y la variable dependiente. Esta manera de representar una función es especialmente interesante cuando la relación f entre la x y la y viene dada por una expresión matemática, pues en ese caso podemos saber con certeza los valores que toma la variable dependiente para cualquier valor que tomemos de la variable independiente. Más aún, si disponemos de una expresión matemática de la función podremos construir con facilidad una tabla de valores de la misma y una gráfica, pues cada pareja de valores (x,y) de la tabla que hagamos representa un punto del plano. Uniendo todos los puntos de la tabla obtendremos la gráfica de la función. |
|
|
A continuación se te da la oportunidad de que elabores una tabla de valores y una gráfica con una función concreta. Al ir dando valores a x irás obteniendo los correspondientes valores de y. Simultáneamente, el punto correspondiente a la pareja de números (x,y), es decir, (x,f(x)) aparecerá representado gráficamente. Al ir dibujando una serie de puntos vamos obteniendo la gráfica de la función. | |
| 3. Ejercicio 1. |
|
Determina cuál es la variable independiente en todas las funciones de los ejemplos anteriores.
|
| 4. Ejercicio 2. | |
|
A continuación se te pide que hagas la representación gráfica de una serie de funciones. Para ello basta con que edites la función que se te pide en la caja de entrada de funciones de la escena siguiente y pulses Intro. Si la gráfica no se ve claramente, puedes probar a cambiar la escala o la posición de los ejes de coordenadas. También puedes representar gráficamente las funciones que tú quieras. Si no sabes muy bien cómo deben introducirse correctamente las expresiones pulsa el botón de ayuda.
| |
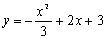 | |
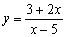 | |
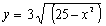 | |
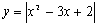 | |
| Elige tú una función | |
| 5. Formas de representar una función. | |
|
Todo lo estudiado en esta página nos permite ver que una función puede ser presentada de múltiples maneras. Resumiendo, una función puede expresarse mediante: Una gráfica. En los ejemplos expuestos la gráfica ha sido de tipo lineal, pero existen multitud de formas gráficas de representación de una función.
Una tabla de valores.
Una frase que exprese la relación entre ambas variables.
Una expresión matemática del tipo y=f(x).
Observación.
Todas las funciones que hemos analizado en los ejemplos son funciones de una variable. Reciben este nombre todas las funciones que sólo tienen una variable independiente. En realidad, el concepto de función es más general. La definición más completa de función habría sido la siguiente: Una función es una ley que relaciona una o más magnitudes (denominadas variables independientes) con otra magnitud (denominada variable dependiente) de forma unívoca, es decir, que a cada conjunto de valores formado por un valor de cada una de las variables independientes le corresponde un valor de la variable dependiente y sólo uno. Una función de varias variables tendría este aspecto: 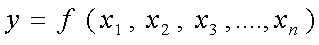 En esta unidad didáctica centraremos nuestro estudio en las funciones de una variable. | |
| José Luis Alonso Borrego | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2001 | ||