FUNCIONES: Elementos de una función.
1º de Bachillerato HH y CCSS. Análisis.
 
Elementos de una función.

Como vimos en el apartado anterior, una función es una manera de relacionar dos magnitudes de forma unívoca. La primera de esas magnitudes se denomina variable independiente y la segunda variable dependiente. Además, hemos visto que toda función (de una variable) admite una expresión del tipo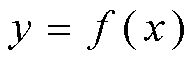

Los dos principales elementos de una función son los posibles valores que pueden tomar ambas variables (dependiente e independiente).

  • Se llama Dominio de una función al conjunto de valores que puede tomar la variable independiente. El dominio de una función del tipo y=f(x) suele representarse con alguna de estas expresiones: D(f), Dom(f).
  • Se llama Recorrido, Rango o Imagen de una función al conjunto de valores que puede tomar la variable dependiente, es decir, es el conjunto de valores que puede alcanzar la función. El recorrido de una función del tipo y=f(x) suele representarse con alguna de estas expresiones: R(f), Rango(f), Im(f).

Vamos a identificar el dominio y el recorrido de las funciones que hemos utilizado para introducir el concepto de función.

EJERCICIO 1.

Vamos a utilizar sólo una de las gráficas del primer ejemplo. Desplazando el punto Pos a lo largo de la gráfica podrás averiguar cuáles son los valores que puede tomar la variable independiente "tiempo" y la variable dependiente "distancia".

Contesta a las siguientes cuestiones:

Dom(f) = [ , ]

Im (f) = [ , ]

EJERCICIO 2.

Selecciona un valor para b. Desplazando el punto x a lo largo de la gráfica podrás averiguar cuáles son los valores que puede tomar la variable independiente "% de población" y la variable dependiente "% de riqueza".

Contesta a las siguientes cuestiones:

Dom(f) = [ , ]

Im (f) = [ , ]

EJERCICIO 3.

Tabla 1.

Temperatura (ºC) del agua 1213141516171819202122232425262728
Nº medio de crías por hembra y día 1.31.51.72.02.32.62.92.82.72.62.42.32.22.01.81.51.1

Observa la tabla anterior y contesta a las siguientes cuestiones:

Dom(f) = [ , ]

Im (f) = [ , ]

EJERCICIO 4.

Ahora vas a determinar el dominio y el recorrido de una serie de funciones matemáticas. Dibuja las gráficas de las funciones que se te indican en la siguiente tabla y halla sus dominios y recorridos. Dibuja, luego las gráficas de las funciones que quieras y halla también sus dominios y recorridos. Pulsa el botón de ayuda si no sabes cómo escribir alguna función.

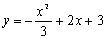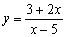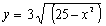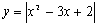Elige tú una función
  Volver al índice   Atrás   adelante  
           
  José Luis Alonso Borrego
 
© Ministerio de Educación y Ciencia. Año 2001