
 |
FUNCIONES: Algunas propiedades de las funciones. |
| 1º de Bachillerato HH y CCSS. Análisis. | |
| 2. Intervalos de monotonía. |
En el apartado anterior hemos definido los conceptos de crecimiento y decrecimiento de una función en un punto. Las propiedades de una función que hacen referencia a puntos concretos reciben el nombre de propiedades locales de la función. Por lo tanto el crecimiento de una función es una propiedad local.
Diremos ahora que una función es creciente (o decreciente en su caso) en un intervalo cuando lo es en todos los puntos de dicho intervalo.
El concocimiento de los intervalos en los que la función crece o decrece proporciona una información de especial interés sobre esa función. Estos intervalos reciben el nombre de intervalos de monotonía de la función. En el ejemplo anterior la función es decreciente en el intervalo (-0'9,4'8) y decreciente en el resto de su dominio. Simbólicamente esto suele expresarse así:
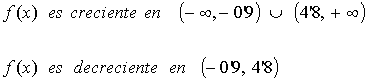 |
| EJERCICIO 1. | |
|
Volvamos a uno de los casos del primer ejemplo de esta unidad didáctica. Determina a partir de la imagen adjunta los intervalos de crecimiento y de decrecimiento de la función que se describe en la gráfica y da una interpretación del significado de que esa función sea creciente o decreciente. | |
|
Cuando una función es creciente (o decreciente en su caso) en todos los puntos de su dominio se dice que la función es monótona (creciente o decreciente). | |
| EJERCICIO 2. | |
|
Utilizando uno de los ejercicios de las páginas anteriores. Dibuja todas las funciones que se te indican al margen y todas las que tú quieras además. Para cada una de ellas determina sus intervalos de monotonía e indica en su caso si se trata de una función monótona o no. | |
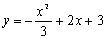 | |
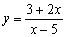 | |
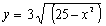 | |
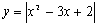 | |
| Elige tú una función | |
| José Luis Alonso Borrego | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2001 | ||