|
"Carlos y D. Juan,
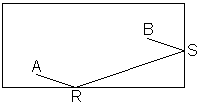
su profesor de matemáticas, están jugando al billar. Al poco tiempo Carlos le pregunta a D. Juan: ¿Qué recorrido tendrá que hacer la
bola A para dar a la bola B después de tocar en dos bandas?"
(Problema extraído del libro "Matemáticas-Algoritmo
3" Vizmanos-Anzola Ed.SM 3ºBUP)
|
|
Una de las reglas básicas en la resolución de
problemas consiste en empezar por lo más fácil: estudiaremos primero como conseguirlo a "una" banda (la inferior)
1.- Mueve por la banda (bien con el ratón o utilizando el
control numérico inferior) el punto R hasta que S coincida con B:
Veamos ahora como obtener la solución,
tanto gráficamente como analíticamente.
GRÁFICAMENTE
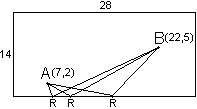
2.- Representa en tu cuaderno la mesa de billar y las bolas.
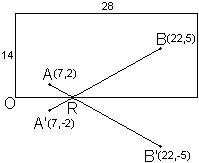
las dimensiones del rectángulo son 28 x 14
"unidades".
el punto A está a 7 u. de la banda izquierda y a 2 u. de
la banda inferior.
el punto B está a 22 u. de la banda izquierda y a 5 u.
de la banda inferior.
|
 |
| El punto R será aquel que verifica que
la suma de distancias a A y B es mínima. |
|
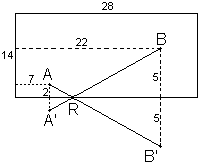
Si no hubiera banda inferior, la bola seguiría hasta el
punto B' (simétrico del B respecto de esa banda), y
d(A,R)+ d(R,B) = d(A,R) + d(R,B') = d(A',R)+d(R,B)
que será mínima cuando A, R y B' estén alineados (en cuyo caso también lo estarán A', R
y B).
a) Representa el punto B'.
b) Representa el segmento AB'.
c) R es la intersección del segmento AB' con la banda inferior.
|
 |
ANALÍTICAMENTE
Fijamos un sistema de referencia con el origen en el extremo
inferior izquierdo, tomando como eje de abscisas la banda inferior y como eje de ordenadas la banda izquierda. De esta forma las coordenadas
del punto A serán (7,2), las de B(22,5) y las de B'(22,-5).
| 3.- a) Encuentra la ecuación de la recta que pasa
por A y B'.
b) Halla la intersección de la recta anterior con
el eje de abscisas.
Sol: R = "7x+15y=79"  "y=0" = (79/7,0) "y=0" = (79/7,0)  (11'286,0) (11'286,0) |
 |
(Nota: Quedaría como ejercicio hacer lo mismo pero suponiendo
que el rebote es en alguna de las otras tres bandas)
|


