Volver a página anterior

Programación lineal

Representación gráfica de la función objetivo

Para hallar, gráficamente, la solución de un problema de programación lineal de dos variables es conveniente seguir este proceso:

  1. Se dibuja el recinto limitado por las restricciones del problema

  2. Se representa una paralela a la función objetivo (igualada a cero)

  3. Se trazan paralelas a la recta anterior que pasen por cada uno de los vértices de la región factible y se observa en que vértice la función z se hace máxima (o mínima).

En la escena siguiente se han representado las restricciones  

 

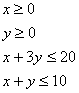
Fíjate en la siguiente escena 4.

 1.-  Maximizar la función objetivo 
sujeta a las restricciones anteriores

Con las mismas restricciones, maximizar los objetivos

2.-
(considerar soluciones 'naturales' y soluciones 'reales')

3.-

4.-

5.-

Cuando la región factible no es acotada es posible que el problema de optimización se quede sin solución. Veámoslo considerando como restricciones: 

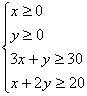
Fíjate en la escena 5, en donde se han representado las restricciones anteriores

1.- minimizar el objetivo

2.-  Maximizar el objetivo

3.-Encontrar el máximo y el mínimo para el objetivo

4.-¿Serías capaz de encontrar una función objetivo que obtuviera un máximo sobre la región factible? Explica la respuesta.

A continuación se deja una escena "en blanco", para que resuelvas los ejercicios de enunciado que se proponen en la libreta de trabajo.

Debes de poner un máximo de tres rectas para las restricciones y la función del objetivo. La región factible debes de sombrearla tú. 

 

              Ir a la página inicial                                                                                         Ir a la página de enunciados

Autor: Juan E. Cereijo Viña

 
© Ministerio de Educación y Ciencia. Año 2001