ÍNDICE Introducción Obxectivos 1. Desigualdades e inecuacións. Clasificación 2. Repaso da función afín. Inecuacións de 1º grao cunha incógnita 3. Repaso da función cuadrática. Inecuacións de 2º grao cunha incógnita 4. Inecuacións de 1º grao con dúas incógnitas 5. Sistemas de dúas inecuacións de 1º grao con dúas incógnitas	INECUACIÓNS
	4º ESO
	INTRODUCCIÓN
	Este tema divídese en 5 partes: 1ª. Concepto de inecuación. 2ª. Repaso das funcións afíns que logo se utilizan para resolver inecuacións de 1º grao cunha incógnita. 3ª. Repaso das funcións cuadráticas e despois a súa utilización para resolver inecuacións de 2º grao cunha incógnita. 4ª. Vese primeiro a solución gráfica das ecuacións con dúas incógnitas e logo as inecuacións de 1º grao con dúas incógnitas. 5ª. Sistemas de dúas inecuacións de 1º grao con dúas incógnitas. Coñecementos previos necesarios Ø Resolver ecuacións de 1º e 2º grao cunha incógnita Ø Representar intervalos na recta real Ø Coñecer o plano cartesiano Ø Manexar a representación de funcións lineais e cuadráticas
	OBXECTIVOS
	Recoñecer inecuacións. Clasificar as inecuacións atendendo o seu grao e ó número de incógnitas. Relacionar as inecuacións de 1º grao cunha incógnita coas gráficas da función afín. Resolver inecuacións de 1º cunha incógnita. Relacionar as inecuacións de 2º grao cunha incógnita coas gráficas da función cuadrática. Resolver inecuacións de 2º grao cunha incógnita. Resolver graficamente inecuacións de 1º grao con dúas incógnitas Resolver graficamente sistemas de dúas inecuacións de 1º grao con dúas incógnitas

1. DESIGUALDADES E INECUACIÓNS. CLASIFICACIÓN

DESIGUALDADES:

Expresións nas que aparece un signo de desigualdade.

Vemos que hai desigualdades nas que soamente aparecen números e outras nas que ademais aparecen letras.

INECUACIÓNS:

Son desigualdades nas que aparecen letras e números coas operacións usuais. As letras son as variables ou incógnitas das inecuacións.

Exemplos de desigualdades:

3 < 7

-2 > -5

x ≤ 2

x-3 ≥ y

Exemplos de inecuacións:

x ≤ 2,

x-3 ≥ y

x²-5x ≤ 4

xy-3 > 0

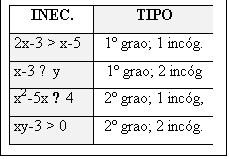
CLASIFICACIÓN DAS INECUACIÓNS

As inecuacións clasifícanse atendendo ó número de incógnitas e ó grao da expresión alxébrica que aparece nelas

ACTIVIDADES PROPOSTAS

1. Copia no teu cuaderrno as seguintes desigualdades, dí cales son inecuacións e indica o seu grao e o número de incógnitas:

a) 2x ≤ -2 b) -3 ≥ 2

c) x²y > 1 d) x²-5y ≤ 0

e) 2x-2y ≥ x-y f) 4(x-3) -2 <2(x-1)

g) x-y² < 2x-y h) 3x³+2y ≥ x²

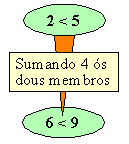
PROPIEDADES DAS DESIGUALDADES

1. Se sumamos ou restamos un mesmo número aos dous membros dunha desigualdade, resulta outra do mesmo sentido.

Exemplos

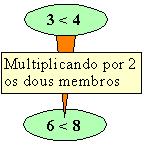
2. Se multiplicamos ou dividimos os dous membros dunha desigualdade por un mesmo número positivo, resulta outra do mesmo sentido.

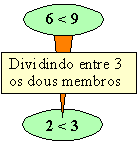
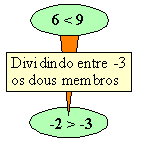
3. Se multiplicamos ou dividimos os dous membros dunha desigualdade por un mesmo número negativo, resulta outra de sentido contrario.

ACTIVIDADES PROPOSTAS

2. Copia no teu cuaderno a seguinte táboa e complétaa escribindo na columna da dereita o resultado de aplicarlle ós dous membros da desigualdade da 1ª columna a operación indicada na segunda:

x-3 > 5	Sumar 3
x+7 > 8	Restar 7
4x < 3	Dividir entre 4
-2x ≥ 8	Dividir entre (-2)
x-9 > -2	Sumar 9
-3x ≤ 9	Dividir entre -3

RESOLVER UNHA INECUACIÓN

Consiste en atopar o valor ou valores da(s) incógnita(s) para os que a desigualdade é certa.

SOLUCIÓNS DUNHA INECUACIÓN

Valores da (s) variable(s) para os que se cumple a desigualdade.

Exemplo

Inecuación: x-3 > 2

Solucións: Tódolos números reais maiores que 5, e dicir

x ∈ (5, ∞)

	Xosé Eixo
	© Ministerio de Educación y Ciencia. Ano 2004