| 2º Bachillerato Ciencias de la Naturaleza y de la Salud y Tecnológico | |
|
|
|
| ÍNDICE | |
|
3.-Elipse 4.-Hipérbola 5.-Parábola 6.-Tangencias Ampliación: Ecuación general de 2º grado
|
|
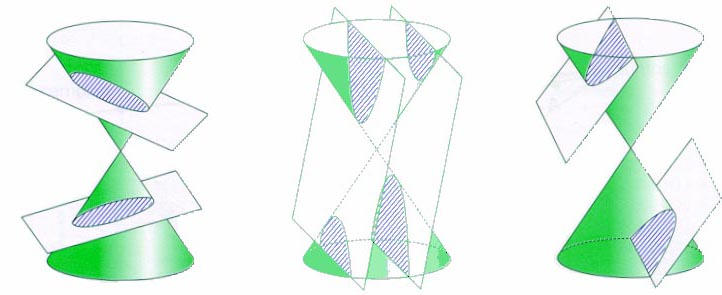
Se llaman curvas cónicas a todas aquellas que se obtienen cortando un cono con un plano. Debido a su origen las curvas cónicas se llaman a veces secciones cónicas.
El matemático griego Menecmo (vivió sobre el 350 A.C.) descubrió estas curvas y fue el matemático griego Apolonio (262-190 A.C.) de Perga (antigua ciudad del Asia Menor) el primero en estudiar detalladamente las curvas cónicas y encontrar la propiedad plana que las definía. Apolonio descubrió que las cónicas se podían clasificar en tres tipos a los que dio el nombre de: elipses, hipérbolas y parábolas.
Las elipses son las curvas que se obtiene cortando una superficie cónica con un plano que no es paralelo a ninguna de sus generatrices.
Las hipérbolas son las curvas que se obtiene al cortar una superficie cónica con un plano que es paralelo a dos de sus generatrices (base y arista).
Las parábolas son las curvas que se obtienen al cortar una superficie cónica con un plano paralelo a una sola generatriz (arista).
Apolonio demostró que las curvas cónicas tienen muchas propiedades interesantes. Algunas de esas propiedades son las que se utilizan actualmente para definirlas.
Quizás las propiedades más interesantes y útiles que descubrió Apolonio de las cónicas son las llamadas propiedades de reflexión. Si se construyen espejos con la forma de una curva cónica que gira alrededor de su eje, se obtienen los llamados espejos elípticos, parabólicos o hiperbólicos, según la curva que gira. Apolonio demostró que si se coloca una fuente de luz en el foco de un espejo elíptico, entonces la luz reflejada en el espejo se concentra en el otro foco. Si se recibe luz de una fuente lejana con un espejo parabólico de manera que los rayos incidentes son paralelos al eje del espejo, entonces la luz reflejada por el espejo se concentra en el foco. Esta propiedad permite encender un papel si se coloca en el foco de un espejo parabólico y el eje del espejo se apunta hacia el sol. Existe la leyenda de que Arquímedes (287-212 A.C.) logró incendiar las naves romanas durante la defensa de Siracusa usando las propiedades de los espejos parabólicos. En la actualidad esta propiedad se utiliza para los radares, las antenas de televisión y espejos solares. La propiedad análoga, que nos dice que un rayo que parte del foco se refleja paralelamente al eje sirve para que los faros de los automóviles concentren el haz en la dirección de la carretera o para estufas. En el caso de los espejos hiperbólicos, la luz proveniente de uno de los focos se refleja como si viniera del otro foco, esta propiedad se utiliza en los grandes estadios para conseguir una superficie mayor iluminada.
En el siglo XVI el filósofo y matemático René Descartes (1596-1650) desarrolló un método para relacionar las curvas con ecuaciones. Este método es la llamada Geometría Analítica. En la Geometría Analítica las curvas cónicas se pueden representar por ecuaciones de segundo grado en las variables x e y. El resultado más sorprendente de la Geometría Analítica es que todas las ecuaciones de segundo grado en dos variables representan secciones cónicas y se lo debemos a Jan de Witt (1629-1672).
Sin lugar a dudas las cónicas son las curvas más importantes que la geometría ofrece a la física. Por ejemplo, las propiedades de reflexión son de gran utilidad en la óptica. Pero sin duda lo que las hace más importantes en la física es el hecho de que las órbitas de los planetas alrededor del sol sean elipses y que, más aún, la trayectoria de cualquier cuerpo sometido a una fuerza gravitatoria es una curva cónica. El astrónomo alemán Johannes Kepler (1570-1630) descubrió que las órbitas de los planetas alrededor del sol son elipses que tienen al sol como uno de sus focos en el caso de la tierra la excentricidad es 0.017 y los demás planetas varían desde 0.004 de Neptuno a 0.250 de Plutón.. Más tarde el célebre matemático y físico inglés Isaac Newton (1642-1727) demostró que la órbita de un cuerpo alrededor de una fuerza de tipo gravitatorio es siempre una curva cónica.
- Recordar la mediatriz y la bisectriz como lugares geométricos.
- Definir la circunferencia como lugar geométrico.
- Determinar la ecuación de una circunferencia conociendo el centro y el radio.
- Calcular la potencia de un punto respecto de una circunferencia y su significado geométrico.
- Calcular el eje radical de dos circunferencias.
- Definir la elipse como lugar geométrico, y conocer sus elementos característicos.
- Conocer la relación fundamental en la elipse.
- Calcular la excentricidad de una elipse y su significado geométrico.
- Definir la hipérbola como lugar geométrico, y conocer sus elementos característicos.
- Conocer la relación fundamental en la hipérbola.
- Calcular la excentricidad de una hipérbola y su significado geométrico.
- Calcular las ecuaciones de las asíntotas de una hipérbola.
- Definir la parábola como lugar geométrico, y conocer sus elementos característicos.
- Calcular las ecuaciones de las rectas tangentes a una circunferencia por un punto de ella o por un punto exterior.
- Calcular las ecuaciones de las rectas tangentes a una elipse por un punto de ella o por un punto exterior.
- Calcular las ecuaciones de las rectas tangentes a una hipérbola.
- Calcular las ecuaciones de las rectas tangentes a una parábola.
- Conocer la relación entre la ecuación general de 2º grado y las distintas cónicas.

