
Presentación Objetivos Contenidos Requisitos Introducción Proyecto Evaluación
Actividades Guiadas
En la siguientes actividades se representan puntos cuyas coordenadas son constantes y puntos que dependen de los controles; también se escriben expresiones asociadas a esos puntos. Dada la frecuencia con la que se utilizan los puntos y la estructura común que tienen todas las herramientas de este nippe, las siguientes actividades son esenciales para la confección de escenas.
Para la edición de las escenas deben seguirse las indicaciones dadas en la primera práctica.
§§§ Abre con el navegador y con el editor de páginas html la página Punto-pendiente.htm de la carpeta Ejercicios, con la que has estado trabajando en la práctica anterior, para modificar las escenas de la página.
§§§ Define en el panel de GRAFICOS de la primera escena un punto fijo A, por ejemplo:
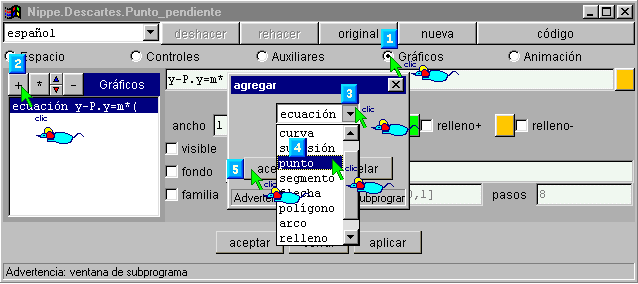
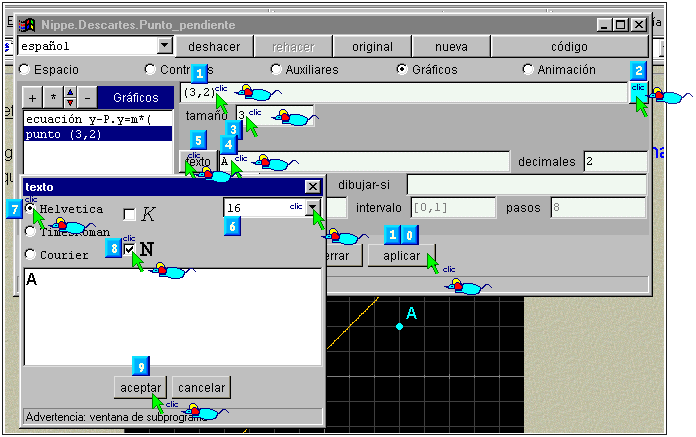
§§§ Define en el mismo panel otros tres puntos fijos B, C, y D, con las mismas características, (basta duplicar el punto A y cambiar las coordenadas y el nombre), por ejemplo:
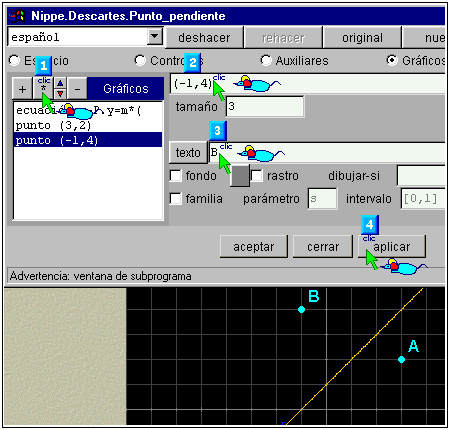
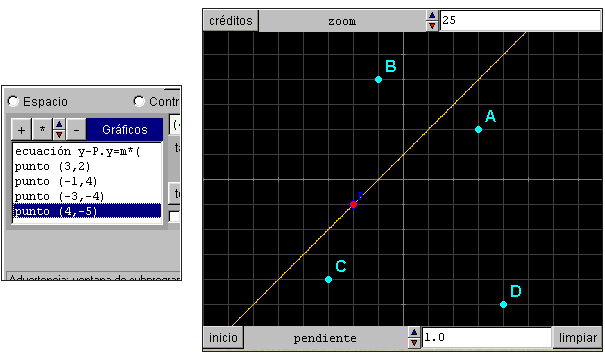
§§§ Añade al final de la actividad dos nuevas propuestas:
2.- Dibuja el haz de rectas paralelas que tienen de pendiente 1; 2 y 1/2.
3.- Dibuja el haz de rectas que pasa por cada uno de los puntos A, B, C y D.
§§§ Observa en la segunda escena el contenido del panel GRÁFICOS, [P.x,P.y] son las coordenadas del punto P y [P.x+t,f(P.x+t)] las de extremo del vector.
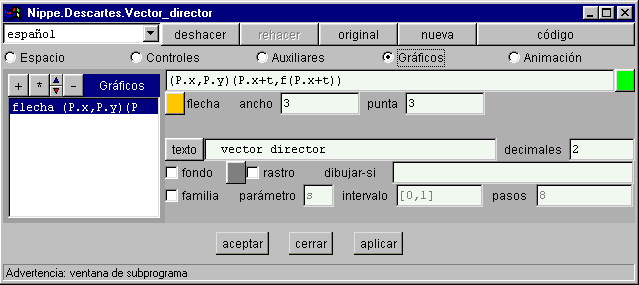
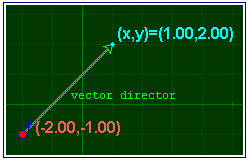
§§§ En la segunda escena representa el texto (x,y) de color azul turquesa en el extremo del vector director.
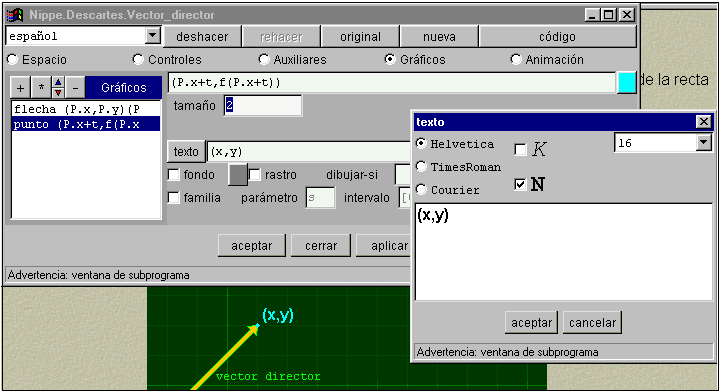
§§§ Modifica la expresión del punto (x,y) para que en el extremo del vector director, además del texto (x,y) escriba también el valor de las coordenadas del punto respectivo. Observa que para que aparezca el contenido de una variable o una expresión en la escena basta escribirla entre corchetes en el campo texto.

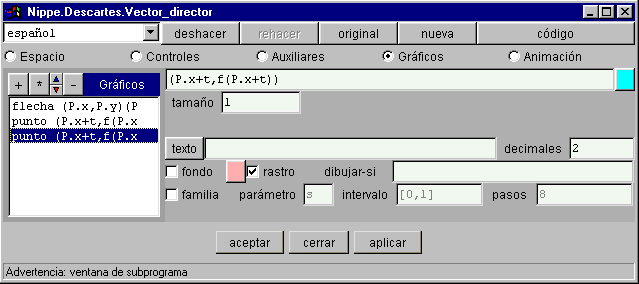
§§§ Duplica el punto (x,y) para que al desplazarse deje un rastro rosa de tamaño 1. Activa el botón Limpiar en el panel ESPACIO, para poder borrar el rastro desde la escena.
![]()
Observa que si se pone el rastro en la instrucción anterior, para no repetirla, resulta que al desplazarse el extremo del vector queda el rastro rosa del extremo, pero también queda rastro del texto asociado a ese punto. Para que sólo quede rastro del punto deberán definirse dos instrucciones, de forma que una escriba la expresión de texto y la otra defina el rastro y el tamaño del rastro. |
§§§ Añade en GRAFICOS la instrucción para que se escriban las coordenadas del punto P, que internamente son P.x y P.y, en color rojo claro.
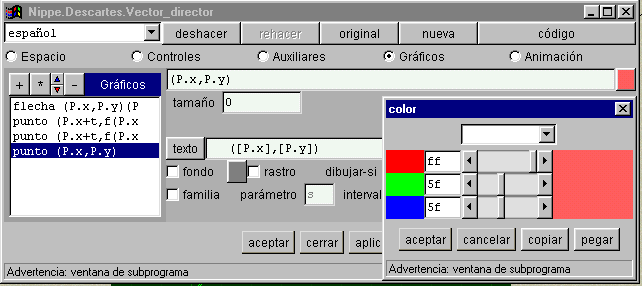
§§§ En la segunda escena selecciona en GRÁFICOS lo primera instrucción y asigna a flecha el color del fondo de la escena, ancho 2 y punta 4.
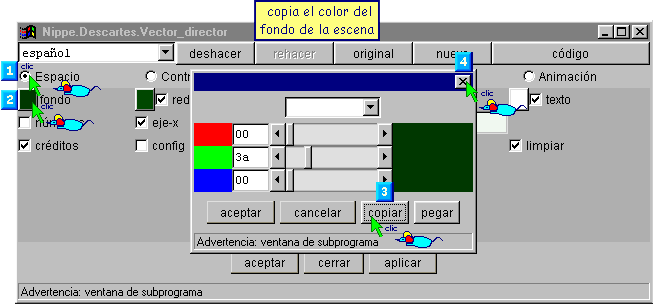
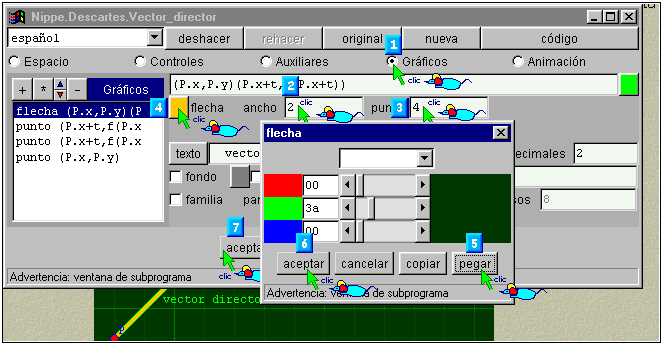
§§§ Guarda los cambios de la segunda escena y copia la segunda actividad completa para crear la tercera actividad de la página Punto-pendiente con el siguiente texto:
| Relación entre
las coordenadas del vector director
y las coordenadas de los puntos P y (x,y) Las coordenadas del vector director son los números que hay que sumar a las coordenadas del origen para obtener las del extremo. |
§§§ En GRÁFICOS de la tercera escena el texto vector director por v y sus coordenadas.

§§§ Representa en la escena de la tercera actividad los segmentos que indican la diferencia de coordenadas entre los puntos P y (x,y) con sus valores respectivos, de color naranja el segmento vertical y amarillo el horizontal.
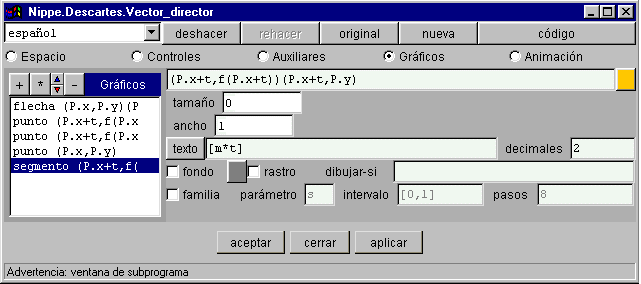
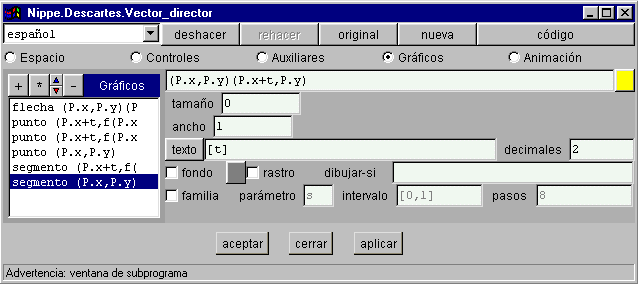
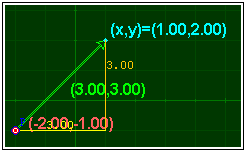
§§§ Comprueba que los números del punto y del segmento horizontal se superponen. Para evitarlo suprime el texto del segmento horizontal y define otro segmento, de ancho cero, que quede por debajo del anterior, para que el número se vea en la parte inferior.
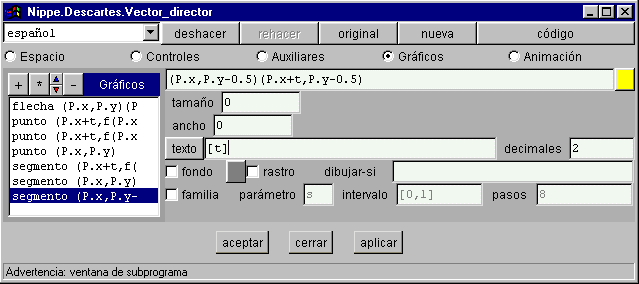
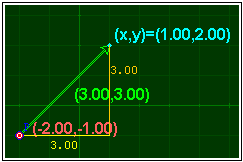
§§§ Asigna el nombre Coordenadas_vector a la escena y copia el código de la escena en la página.
§§§ Escribe como propuesta de trabajo el siguiente texto:
5.- Comprueba que las coordenadas del extremo menos las del origen dan las coordenadas del vector director, sean cuales sean los puntos y la pendiente que elijas.
§§§ Copia la tercera actividad de Punto-pendiente para crear la cuarta actividad con el siguiente texto:
| Relación entre
cualquier vector
director de una
recta y su pendiente (m) El cociente de la ordenada entre la abscisa de cualquier vector director de una recta concreta siempre da el mismo resultado. |
§§§ En GRÁFICOS define cinco instrucciones de texto, que den lugar al siguiente código:

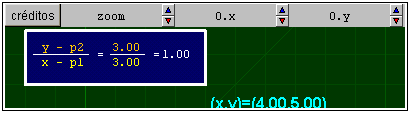
en la escena deberá aparece la expresión siguiente:

§§§ Observa que la expresión se ha escrito por filas y que las rayas de las fracciones se han hecho con el signo de subrayado, que queda a distinta altura que el signo de igualdad, por ello hay que poner estas expresiones en líneas diferentes y con distintas coordenadas.
§§§ Escribe como propuesta de trabajo de la cuarta actividad el siguiente texto:
6.- Observa las coordenadas del vector de dirección e intenta encontrar una relación entre esas coordenadas y la pendiente de la recta. (Elige una pendiente y prueba con distintos puntos de la misma recta. Después comprueba tus hipótesis con diferentes rectas).
§§§ En la cuarta actividad define un rectángulo sobre la zona en la que está la expresión de la actividad anterior, de forma que quede resaltada. Por ejemplo:
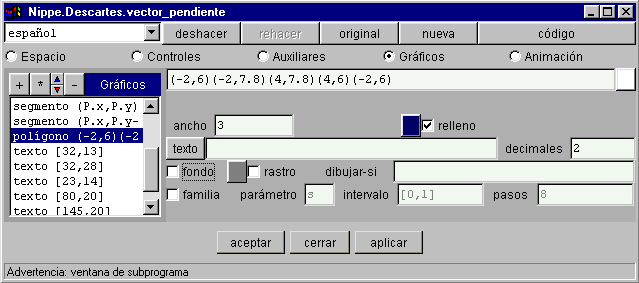
§§§ Observa que si se cambia la escala o los ejes el rectángulo queda afectado y la expresión no, eso se debe a que las coordenadas de las figuras que se representan son coordenadas relativas a la posición del origen de coordenadas y la escala utilizada, mientras que las coordenadas del texto son absolutas respecto del vértice superior izquierdo de la escena. En la siguiente práctica se definirán funciones auxiliares para resolver este problema.
En las siguientes actividades se comprueba la facilidad que tiene el nippe Descartes para escribir y representar funciones dadas por sus ecuaciones cartesianas.
§§§ Analiza el contenido de la primera instrucción del panel GRÁFICOS de la primera escena. Observa que si se escribe la la ecuación explícita y=m*(x-P.x)+P.y la recta se representa mejor. Define la ecuación explícita y guarda la escena de esta forma.
§§§ Añade a la ventana GRÁFICOS de las escenas segunda, tercera y cuarta, de la página Punto-pendiente, la ecuación siguiente, para que se muestre la recta de pendiente m que pasa por P, asígnale un color tenue, para que quede difuminada y haz que no aparezca su ecuación en la escena.
y=m*(x-P.x)+P.y
§§§ Guarda las escenas modificadas y el archivo Punto-pendiente.htm, con el que has estado trabajando, con los cambios realizados hasta ahora.
§§§ Como no conviene que una misma página tenga muchas escenas, crea un nuevo archivo copiando y pegando el archivo anterior y ponle el nombre Punto-pendiente_2.htm, para incluir en él nuevas actividades.
§§§ Añade al enunciado de cada actividad en números romanos el orden que ocupa para poder referirse a ellas.
§§§ En el nuevo archivo Punto-pendiente_2.htm sustituye la primera actividad, por la quinta actividad con el siguiente texto:
| V. Ecuación de
la recta que pasa por P
y tiene de pendiente m En la actividad anterior habrás obtenido que el cociente de la ordenada entre la abscisa de cualquier vector director es precisamente la pendiente de esa recta. Por lo tanto si (p1,p2) son las coordenadas de P, (x,y) es un punto cualquiera de la recta y m su pendiente se verifica que: |
§§§ Utiliza un programa de dibujo o algún sistema de edición para insertar en la página la siguientes expresiones:

§§§ En la escena correspondiente a esta actividad haz que la ecuación de la recta que hay definida no deje rastro, que tenga un color difuminado, gris o similar, para que sirva como referencia, y añade la ecuación y-1=2(x-3) de color amarillo y que sea editable. Añade también un texto en [10,10] que ponga la letra P y las coordenadas de P en color turquesa.
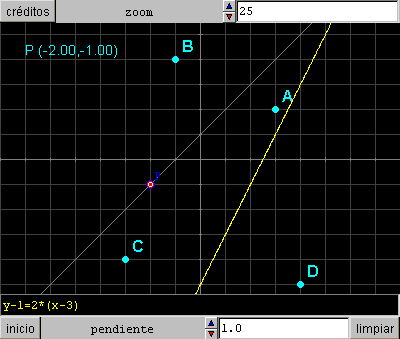
§§§ Asigna un nombre apropiado a la escena y guárdala en la página html. Cambia también el nombre a la página html, como se indicó en la primera práctica.
§§§ Escribe como propuesta de trabajo el siguiente texto:
7.- Escribe la ecuación de la recta de la que se conocen las coordenadas de un punto por donde pasa y su pendiente. (Para cada caso coloca el punto P en la posición que se indica y escribe el valor de la pendiente m, con lo que tendrás la referencia de la recta que se debe representar, luego escribe la ecuación y comprueba si coincide).
a) pasa por A y m=2 b) pasa por A y m=3 c) pasa por B y m=1/2 d) pasa por B y m= -1/2 e) pasa por C y m=12/7 f) pasa por C y m= -2 g) pasa por D y m= -1 h) pasa por D y m=0
prueba con otros puntos y las pendientes que quieras.
§§§ Borra el resto de las actividades y escenas de esta página.
§§§ En la página Punto_pendiente.htm añade al final un texto o un gráfico que conduzca, mediante un hipervínculo, a la página Punto-pendiente_2.htm. Para ello basta escribir el texto o el gráfico, seleccionarlo, pulsar la opción o el icono de crear hipervínculo e indicar como destino la página Punto-pendiente_2.htm.
§§§ Guarda las dos páginas con los cambios realizados y comprueba que las escenas y el hipervínculo funcionan.
En las siguientes actividades se utilizan los dos modos posibles de representar arcos con el nippe Descartes. En el caso en que se requiere determinar los ángulos, se ha usado la función arco tangente, aunque aún no se ha tratado el apartado de las funciones.
§§§ Copia la quinta actividad de Punto-pendiente_2 para crear, a continuación, la sexta actividad con el siguiente texto:
| VI. Relación
entre el ángulo de una recta y su pendiente Se llama ángulo de una recta al que forma esa recta y el semieje OX positivo. |
§§§ En el panel ESPACIO de la escena de esta actividad activa las casillas red y red10. En GRÁFICOS elimina los puntos A, B, C, D y la ecuación que dibuja la recta amarilla; sustituye, también, el contenido del texto que escribe las coordenadas del punto P por la expresión que refleje el ángulo de la recta, por ejemplo ángulo = [atan(m)] rad y observa que al modificar la pendiente se van actualizando los valores de ángulo en radianes (atan es la función arco tangente).
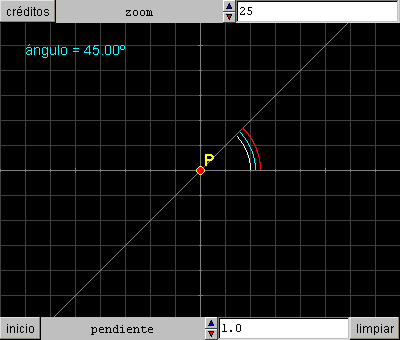
Para dibujar el arco correspondiente al ángulo hay que expresar el ángulo en grados sexagesimales, por lo que se escribirá la expresión atan(m)*180/3.1416.
§§§ Sustituye la expresión del texto en GRÁFICOS para que se muestre el ángulo en grados:
ángulo = [atan(m)*180/3.1416]º
§§§ Añade en GRÁFICOS la instrucción que dibuje un arco con centro en el punto P, con radio 2, valor inicial 0 y final el ángulo atan(m)*180/3.1416 de color blanco.
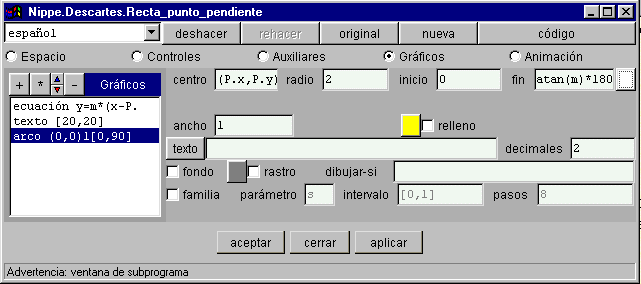
§§§ Comprueba cómo se representan los arcos para valores positivos y negativos de la pendiente. Eso se debe a que la función arco tangente devuelve un valor del intervalo (-pi/2,pi/2) en radianes, es decir (-90,90) expresado en grados. Se verá más adelante cómo se puede resolver que el valor esté en el intervalo (0,180) usando las funciones.
§§§ Dibuja otro arco, de color turquesa, en la misma escena, usando la otra forma de representación, en la que se necesitan tres puntos:
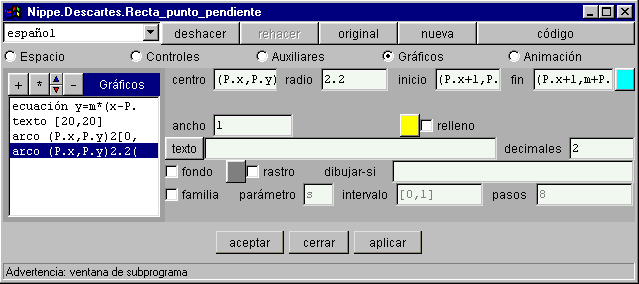
En este caso sí es posible representar el ángulo en el intervalo (0,180) si hacemos depender el tercer punto de la pendiente, de forma que quede a un lado u otro de la recta según sea el signo de m, por ejemplo (P.x+m,m^2+P.y).
Con esta expresión puede haber problemas cuando m=0, ya que el primer punto y el tercero son iguales y se representa un ángulo de 90º. Para evitarlo se puede añadir un condición a la representación abs(m)>0.001, ya que con la precisión que se está trabajando es suficiente que el valor absoluto de la pendiente sea mayor que una milésima.
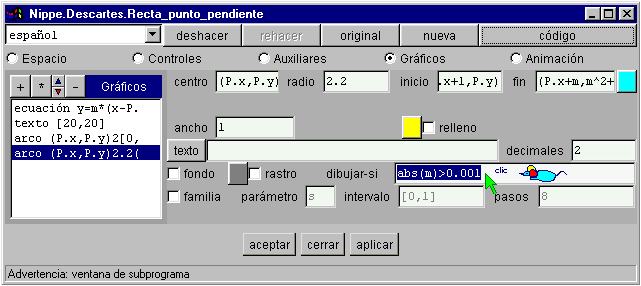
§§§ Añade como propuesta de trabajo para esta actividad:
8.- Observa el ángulo que forma cada recta, cuando se cambia la pendiente.
La actividad se completará en las siguientes prácticas.
En las siguientes actividades se usa la herramienta curvas como herramienta auxiliar, que suele resultar muy útil para hacer representaciones de arcos de cónicas, semirrectas, segmentos, curvas, etc.
§§§ En el panel de GRÁFICOS de la sexta actividad define una curva de color rojo definida por las coordenadas paramétricas (2.4*cos(t),2.4*sen(t)), donde t es el parámetro que toma 200 valores en el intervalo (0,atan(m)).
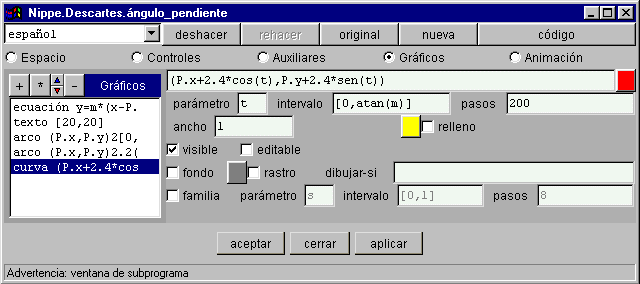
Se han usado las coordenadas paramétricas de una circunferencia para un radio de 2.4. En este caso la representación sólo se hará para los valores del ángulo entre cero y el ángulo de la recta. Como en la actividad anterior, queda por resolver el problema del intervalo del arco tangente.
§§§ Observa que el ángulo se representa tomando como centro el origen de coordenadas, para que lo haga desde el punto P traslada las coordenadas: (P.x+2.4*cos(t),P.y+2.4*sen(t)).
§§§ Desactiva la opción visible para que no se muestre en la escena.
Para representar la semirrecta horizontal, a partir del punto P, que sirva de lado del ángulo, se puede usar también esta herramienta.
§§§ Representa la semirrecta horizontal de color gris que sirva como lado inicial de los ángulos usando la herramienta curvas.
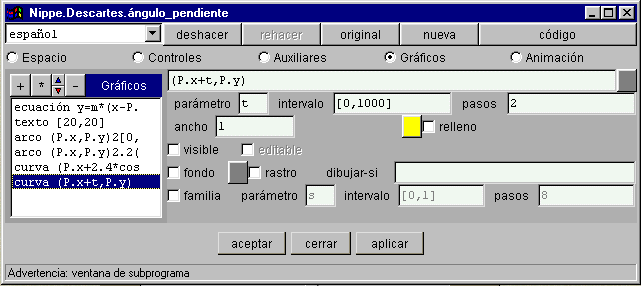
§§§ En el panel CONTROLES de la primera escena de la página Punto-pendiente modifica el control para que se vea mejor la letra, por ejemplo: color naranja y tamaño 16. Asigna el mismo color y el mismo tamaño al texto correspondiente del panel de GRÁFICOS.
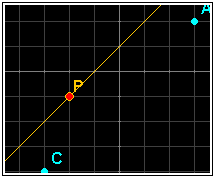
§§§ En las escenas segunda, tercera y cuarta de la página Punto-pendiente modifica el control para que la letra P tenga el mismo color que el texto de sus coordenadas que se definen en el panel de GRÁFICOS. Suprime la instrucción de GRÁFICOS que escribe sus coordenadas y haz que se escriban difiniéndolas en el campo texto del propio control gráfico.
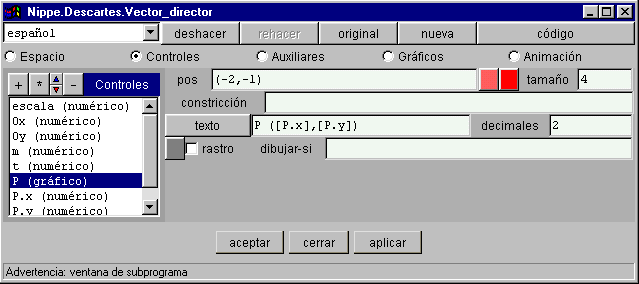
§§§ En la cuarta escena cambia también la posición inicial del control P para que esté en el primer cuadrante y suprime los controles numéricos P.x y P.y
§§§ En la actividad quinta de la página Punto-pendiente (2) haz que aparezcan las coordenadas del control gráfico P en la parte inferior de la escena, como parámetros, para facilitar la colocación del control en el lugar que se desee. Para ello, en el panel CONTROLES selecciona los controles numéricos P.x y P.y y asígnales de nombre p1 y p2, respectivamente. Desactiva el botón limpiar de la escena.
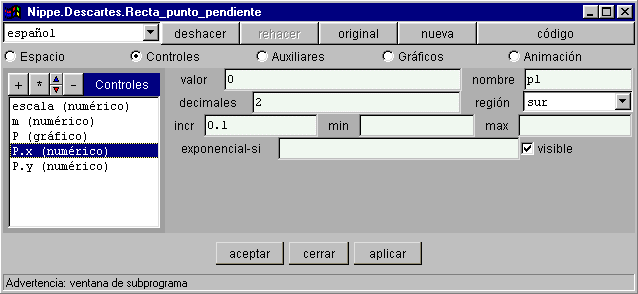
Esto hará que aparezcan como parámetros p1 y p2, que podrán modificarse usando los pulsadores o escribiendo el valor correspondiente y pulsando la tecla Intro.
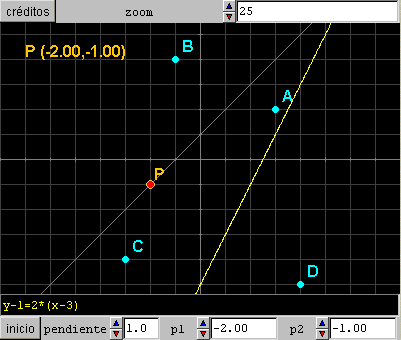
Para que se vea con más claridad el ángulo de la recta de la sexta actividad se restringe al control P para que se mueva sólo sobre el semieje horizontal.
§§§ En la sexta escena abre el panel CONTROLES, modifica en el control gráfico P el punto inicial para que sea (0,0), escribe la función de constricción y = 0 y pon color amarillo al borde exterior y mayor tamaño al campo de texto.
§§§ Observa que al desplazar el control sólo se mueve por el eje de abscisas.
§§§ Guarda las páginas Punto pendiente y Punto pendiente (2).htm con todos los cambios realizados.
En las siguientes actividades se van a utilizar las sucesiones para generar una cuadrícula de puntos, que sustituya a la cuadrícula normal.
§§§ En la quinta actividad de la página Punto-pendiente (2) desactiva en el panel ESPACIO las casillas de red y red10 y define una sucesión como la que se indica en la figura :
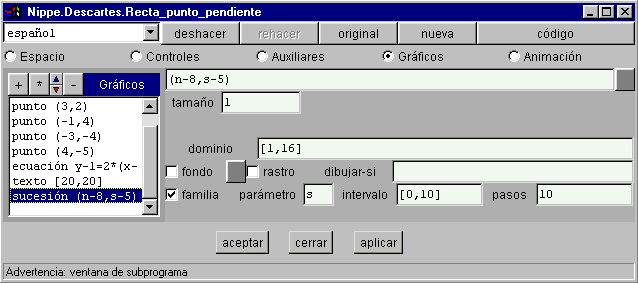
Se usan dos parámetros para hacer una cuadrícula de puntos: la n, que es la variable de este panel, representa los puntos de cada línea horizontal y la s, que es el parámetro que cambia la ordenada, hace que se representen las distintas líneas de la escena.
§§§ Comprueba que se obtiene una imagen como la siguiente:
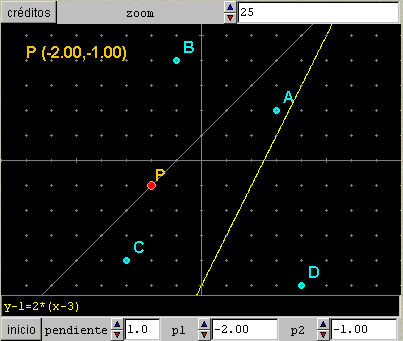
§§§ En el panel GRÁFICOS de la cuarta escena de la página Punto-pendiente añade la instrucción de relleno del triángulo que forma el vector y los dos segmentos dibujados, por ejemplo:
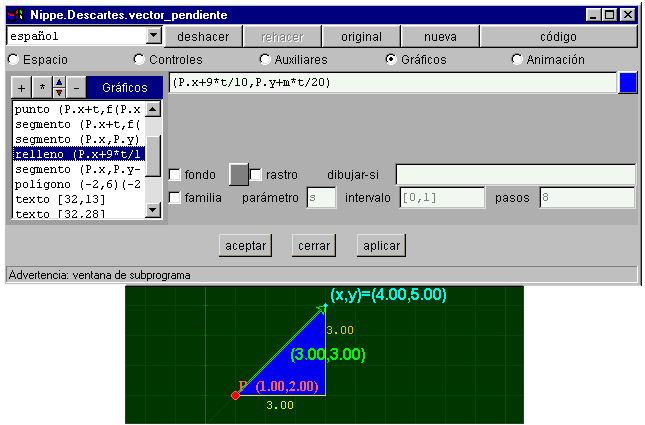
Presentación Objetivos Contenidos Requisitos Introducción Proyecto Evaluación
| Juan Madrigal Muga | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2002 | ||